Определение области видимости объекта на плоскости среди препятствий

 

ВВЕДЕНИЕ

         Для того, чтобы определять какие области нужно показывать игроку во время игры, мы будем использовать многоугольник видимости. Многоугольник видимости – это многоугольная область всех точек плоскости, видимых из определенной точки. Данный способ применяется в робототехники, для определения наилучшего расположения охраны в картинных галереях, а также в компьютерных играх, на примере которых мы и будем рассматривать этот метод.

         Несколько важных определений:

·        Если многоугольник видимости ограничен, то он является звёздчатым многоугольником.

·        Многоугольник видимости ограничен, если все лучи, проведённые из точки, в конце концов, обрываются на некотором препятствии.

 

АЛГОРИТМЫ РЕАЛИЗАЦИИ

 

         Алгоритм лучей

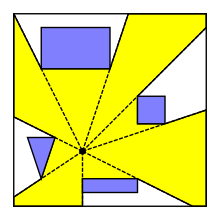
    Самым простым, и легким для старта, способом расчета данного многоугольника является направление лучей из центра во все стороны. Чтобы упростить эту задачу можно направлять лучи только под углами которые соприкасаются с углами препятствий. А полученные таким образом треугольники будут являться видимыми областями.

             Алгоритм следующий:

·        Вычислить углы начала и конца стен

·        Провести луч из центра касательно каждого угла

·        Заполнить получившиеся треугольники

          Следующим шагом будет определение через какие стены проходит луч, нам должна быть видна только ближайшая стена. Будем определять ее с помощью расчета расстояния от центра до точки, оставляя только лучи с наименьшим расстоянием до объекта или проходящие сквозь него. Также нам требуется ограничить общую область видимости игрока кругом с затухающим светом в конце.

       Существуют еще несколько алгоритмов определения многоугольника види-мости такие как: алгоритм для точек в простом многоугольнике, алгоритм для точек среди отрезков.

 

         Алгоритм для точек в простом многоугольнике

         Рассмотрим алгоритм для точек в простом многоугольнике описывается так: мы проходим границу многоугольника P последовательно перебирая вершины и сохраняя их последовательность S = s₁, s₂,…,s_t ,все эти вершины должны быть видимы из нашей точки p. Если обнаружится, что какая-то новая вершина перекрывает добавленную вершину в S, то перекрытая вершина удаляется. Алгоритм прекращает работу после обхода всех вершин.

 

         Алгоритм для точек среди отрезков

         Следующими рассматриваемыми нами алгоритмами будут для точек среди отрезков. Таких алгоритмов существует несколько, поэтому мы рассмотрим парочку из них и опишем их.

 

         Алгоритм Сазерленда-Коэна

         Первым из таких будет алгоритм Сазерленда- Коэна. Он представляет собой отсечение отрезка, при котором отрезок с концами в точка p₁ = (x₁,y₁), p₂=(x₂,y₂) поочередно разбивается прямыми проходящими через него, из изначальной точки p, на две части. Затем, та часть которая оказывается за областью видимости (перекрывается другим объектом) отбрасывается, а точка разбиения становится новым концом, так происходит до тех пор, пока ни одна из частей не будет перекрываться другим отрезком.

        

         Алгоритм углового выметания

         Алгоритм углового выметания основывается на заметающей прямой. С лева на право будет двигаться линия которая будет рассматривать прошедшие собой точки до которых будет строиться отрезок от изначальной точки просмотра p. Этот алгоритм похож на алгоритм рассмотрения всех углов, но с существенным отличием, нам не приходится строить множество лучей вокруг точки разбивая пространство на большое количество треугольников.

 

         Вывод

         Все алгоритмы поиска области видимости относительно похожи друг на друга, и каждый из них можно использовать для любой вашей задачи. Такое множество существующих методов дает возможность выбора в зависимости от поставленной задачи и ее постановки, а также вашего личного вашего усмотрения.